Plan De Travail
Introduction générale
CHAPITRE I
:Matériaux hétérogènes et lois de mélange
vMélange hétérogène
vTypes de mélanges
vLes matériaux utilisés
vLes lois des mélanges
CHAPITRE II : Réseaux de neurones
vPrincipe des réseaux de neurones
formels
vLa fonction d’activation
vLes différents types de réseaux de
neurones
CHAPITRE III :Résultats et discussions
vApplication sur différents mélanges
binaires
Application de la loi de Bottreau
vApplication des réseaux de
neurones
vConclusion générale
CHAPITRE I
Matériaux hétérogènes et lois de mélange
I.1 Introduction :
Plusieurs études sont envisagées
pour décrire le comportement diélectrique des matériaux hétérogènes à partir
des caractéristiques diélectriques de leurs constituants.
Dans ce chapitre, nous nous sommes intéressés
à étudier divers notions sur les matériaux hétérogènes. Nous essayerons
rappeler quelques principes relatifs à la polarisation des milieux diélectriques et nous citerons
quelques lois classiques
I.2 Mélange hétérogène :
Un mélange hétérogène [1] est un agrégat formé de
grains d'un ou plusieurs corps purs (inclusions), répartie dans un milieu continu
(matrice), un tel agrégat est caractérisé par sa compacité qui présente le
rapport du volume de grains, au volume total de l'agrégat:
 | |
| (I.1) |
Avec:
M : La compacité ;
Vgrains
: Volume des grains ;
Vagrégat : Volume de l'agrégat ;
Les milieux entrant dans la composition de ces
mélanges ne doivent évidemment pas interagir entre eux (réactions chimique). La
figure (Fig.I.1) présente un mélange hétérogène constitué de deux phases
(matériau N°1 : matrice) et (matériau N°2 : inclusion)
Fig I.1
: Mélange
hétérogènes binaire
I.2.1 Types de mélanges :
La permittivité d'un tel mélange
[2] dépend de la permittivité propre des constituants. Leurs
proportions en volume, la forme de grains et leurs orientations.
Les mélanges peuvent être classés
en deux catégories:
v Mélanges
réseaux : Ce sont
des mélanges formés de grains ayant la même forme, même dimension et la même
orientation. Pour que les interactions restent faibles il faut que la forme des
grains soit simple et les mélanges soient suffisamment dilués.
v Mélanges
statistiques : Ce sont des mélanges dans lesquels les grains sont de forme et de dimension
quelconques et sont répartis au hasard.
I.3
Étude de la permittivité diélectrique :
Les milieux matériels sont généralement
caractérisées par trois paramètres : la
permittivité (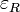 ), la conductivité (σ) et la perméabilité (μ).
), la conductivité (σ) et la perméabilité (μ).
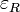 ), la conductivité (σ) et la perméabilité (μ).
), la conductivité (σ) et la perméabilité (μ).
Ils sont classés en deux grandes classes : les
conducteurs (tel que les Noirs,..
…etc.) et les isolants
(diélectriques : tel que les Polymères, …etc.). Les descriptions des diélectriques sont plus complexes que
celle des milieux conducteurs. Le
matériau lui même, est souvent formé de dipôles qui sont susceptibles de varier
en orientation et en valeur en fonction de champ électrique appliqué.
Tous les matériaux diélectriques ont en commun leur
aptitude à emmagasiner l’énergie électrique [9]. Ce phénomène est rendu
possible par le déplacement d’un champ électrique appliqué .Ce mécanisme de
déplacement des charges, ou polarisation,
est différent suivant le type de diélectrique et la fréquence de champ
électrique.
Les diélectriques [10, 11, 12] parfait ne possèdent
pas des charges électrique libres. Ils ont une conductivité nulle.
Cependant, les diélectriques réels sont caractérisés
par leurs constante diélectrique complexe :
et une conductivité
de très faible valeur et par conséquent présentent des pertes diélectriques. On
distingue deux types de diélectriques :
·
Diélectrique
polaire : Caractérisé par l’existence d’un
moment dipolaire permanent résultant de l’asymétrie des molécules du
diélectrique (géométriquement les barycentres des charges ne coïncident pas).
·
Diélectrique
non polaire : Ce
diélectrique ne présent aucune asymétrie, ce milieu se polarise par déformation
des molécules sous l’effet d’un champ électrique. Il résulte des moments
dipolaires induits.
Les propriétés des milieux diélectriques sont:
Ø Linéarité :
Lorsque la propriété diélectrique ε de milieu
est indépendante de l’intensité du champ électrique appliqué, ce milieu est dit
linéaire :
 (I.2)
(I.2)
Avec :
 : Vecteur de déplacement ;
: Vecteur de déplacement ;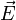 : Champ électrique appliqué ;
: Champ électrique appliqué ; :
Permittivité diélectrique du milieu ;
:
Permittivité diélectrique du milieu ;
Ø
Homogénéité :
Lorsque la permittivité reste constante et
indépendante des coordonnées spatiales d’un point dans le milieu, le
diélectrique est dit homogène.
Ø
Isotropie :
Un milieu est dit isotrope lorsque sa permittivité est indépendante de la direction du champ
électrique appliqué.
I.4 Phénomène de polarisation :
C’est l’expérience de Faraday [13, 12, 25] qui a
permis de mettre en évidence le phénomène de polarisation. Cette expérience est
réalisée sur un condensateur où un insert diélectrique est placé entre les deux
armatures.
Dans le vide, la quantité de charges par unité de
surface sur les plaques du condensateur vaut:
(I.3)
Avec :
d : Distance entre les plaques ;
V : Tension appliquée ;
 :Permittivité du vide ;
:Permittivité du vide ;
Si l’on introduit entre les plaques de condensateur
un matériau diélectrique (Fig.I.2), cette densité surfacique de charge
s’accroît et l’on obtient :
(I.4)
La grandeur (ε) est une
Caractéristique du matériau, elle est appelée constante diélectrique, elle est,
reliée à la permittivité du vide par :
 (I.5)
(I.5)
Avec :
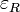 :
Constante relative du matériau;
:
Constante relative du matériau;
Fig. I.2 : Expérience de Faraday.
Si on appelle P
l’accroissement de densité surfacique de charges et en définissant la
susceptibilité diélectrique par : 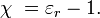
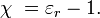
On
obtient les relations :
(I.6)
Si
on l’exprime en l’onction du vecteur déplacement électrique  défini par :
défini par :
 défini par :
défini par : (I.7)
(I.7)
On
obtient la relation :
(I.8)
Le mécanisme de déplacement des charges, où
polarisation est différent suivant le type de diélectrique et la fréquence du
champ électrique [2,9, 13]. On distingue quatre types de polarisation
diélectrique. Dont les effets extrêmes sont variés. Les éléments microscopiques
sont à l’échelle de la molécule, de l’ion et de l’atome.
Le champ appliqué provoque une séparation spatiale
des charges de signes opposés. La fréquence d’un champ alternative détermine le
type de polarisation dominant: les éléments lourds (zone
de diélectrique) résonnent a basse fréquence. Les éléments légers (échelle
atomique). Résonnent à très haute fréquence.
I.4.1
Polarisation inter-faciale (effet Maxwell-Wagner-Sillars) :
Ce type de polarisation [7] apparaît dans les
matériaux hétérogènes. Il provient de l‘accumulation de charges aux interfaces
entre les différentes phases constituant les matériaux lorsque ces différentes
phases ont des permittivités et des conductivités différentes, C’est par
exemple le cas d’un polymère (tel que le polyéthylène) contenant Une charge de
conductivité appréciable (telle que le noir de carbone), L’application du champ
électrique fait apparaître aux interfaces polymère-charge des charges
électroniques. Ce type de polarisation est encore appelé effet
Maxwell-Wagner-Sillars, et se manifeste en basse fréquence suivant
suivant la conductivité de la charge.
Aux pertes induites par polarisation inter-faciale
s’ajoutent les pertes par conduction ionique observées essentiellement à haute
température, et basse fréquence. Ces pertes par conduction sont identifiables. Figure (I.3. a).
I.4.2
La polarisation par orientation (dipolaire) :
Cette polarisation [9] se manifeste dans les milieux
dont les molécules possèdent un moment dipolaire permanent. Sous l’effet d’un
champ électrique externe, ces moments ont tendance à s’orienter dans le sens de
celui ci. Cette polarisation se produit dans une gamme de fréquence plus
élevée. Figure (I.3.b).
I.4.3
La polarisation ionique :
Cette polarisation a lieu dans la
gamme des infra rouges. Elle est la conséquence du déplacement relatif des
atomes ou des ions par rapport à leurs positions d’équilibre, Figure (I.3.c).
I.4.4
La polarisation électronique :
Elle se produit à des fréquences très élevées,
situées vers l’ultraviolet. Les nuages atomiques (positifs) étant supposés
fixes dans la structure diélectrique. Ce sont les nuages électroniques qui se
déplacent dans la direction du champ appliqué, Figure (I.4.d).
Fig. I.3:
Les différents types de polarisation
[11]
a suivre











جيد
RépondreSupprimer