Fourier Transform

1. Introduction to the Fourier Transform Virtually everything in the world can be described via a waveform - a function of time, space or some other variable. For instance, sound waves, electromagnetic fields, the elevation of a hill versus location, a plot of VSWR versus frequency, the price of your favorite stock versus time, etc. The Fourier Transform gives us a unique and powerful way of viewing these waveforms. The purpose of this entire website is to explain the following fundamental fact: One of the Fundamental Secrets of the Universe All waveforms, no matter what you scribble or observe in the universe, are actually just the sum of simple sinusoids of different frequencies. The above fact, is exceedingly cool, as we will see. The Fourer Transform decomposes a waveform - basically any real world waveform, into sinusoids. That is, the Fourier Transform gives us another way to represent a waveform. (Need a refresher on sinusoids? See Sinusoid Properties) As an example, lets break down the waveform in Figure 1 into its 'building blocks' (or constituent frequencies). This decomposition can be done with a Fourier transform (or Fourier series for periodic waveforms), as we will see. 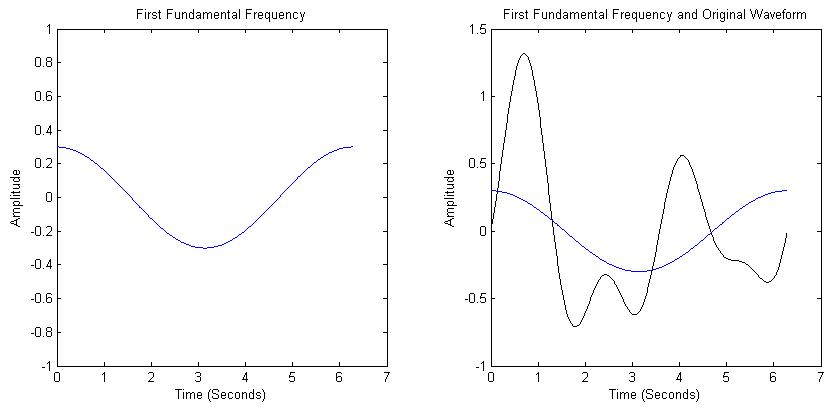The first component is a sinusoidal wave with period T=6.28 (2*pi) and amplitude 0.3, as shown in Figure 1.

Figure 1. First fundamental frequency (left) and original waveform (right) compared.

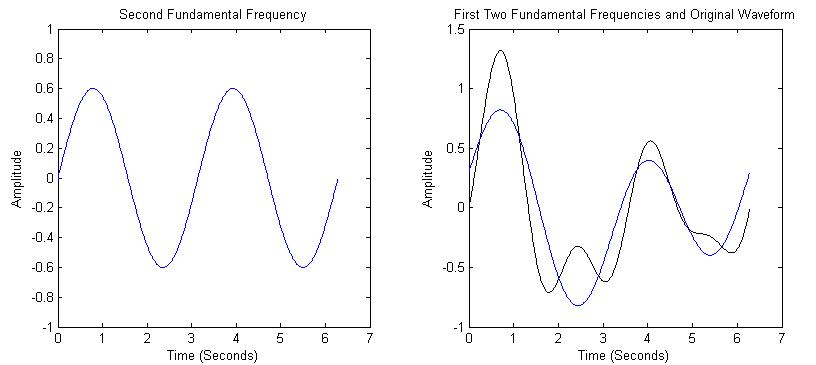
The second frequency will have a period half as long as the first (twice the frequency). The second component is shown on the left in Figure 2, along with the sum of the first two frequencies compared to the original waveform.

Figure 2. Second fundamental frequency (left) and original waveform compared with the first two frequency components.

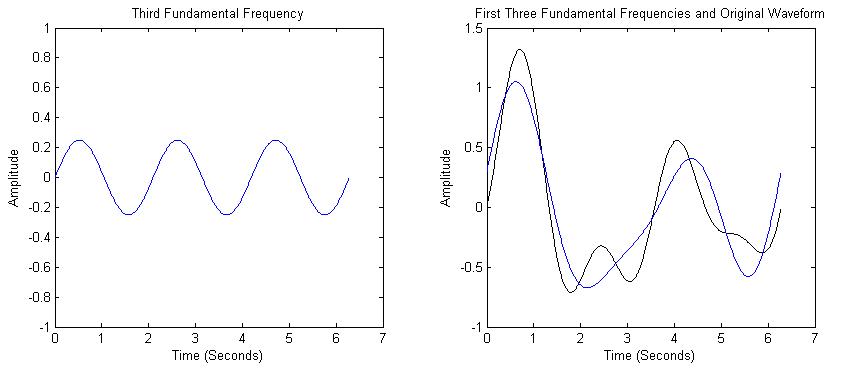
We see that the sum of the first two frequencies is starting to look like the original waveform. The third frequency component is 3 times the frequency as the first. The sum of the first 3 components are shown in Figure 3.

Figure 3. Third fundamental frequency (left) and original waveform compared with the first three frequency components.

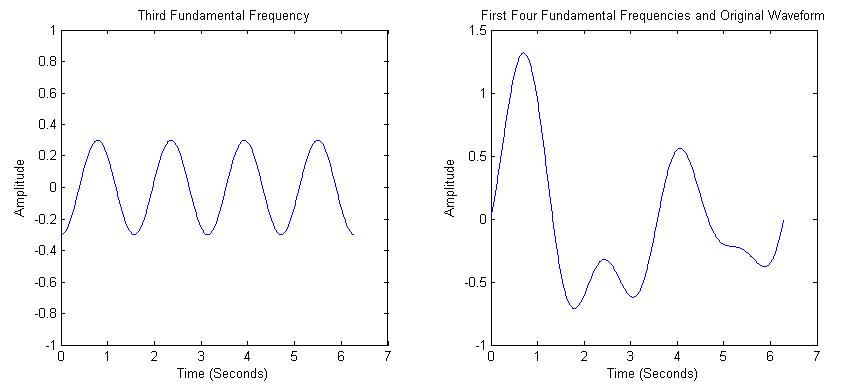
Finally, adding in the fourth frequency component, we get the original waveform, shown in Figure 5.

Figure 5. Fourth fundamental frequency (left) and original waveform compared with the first four frequency components (overlapped).